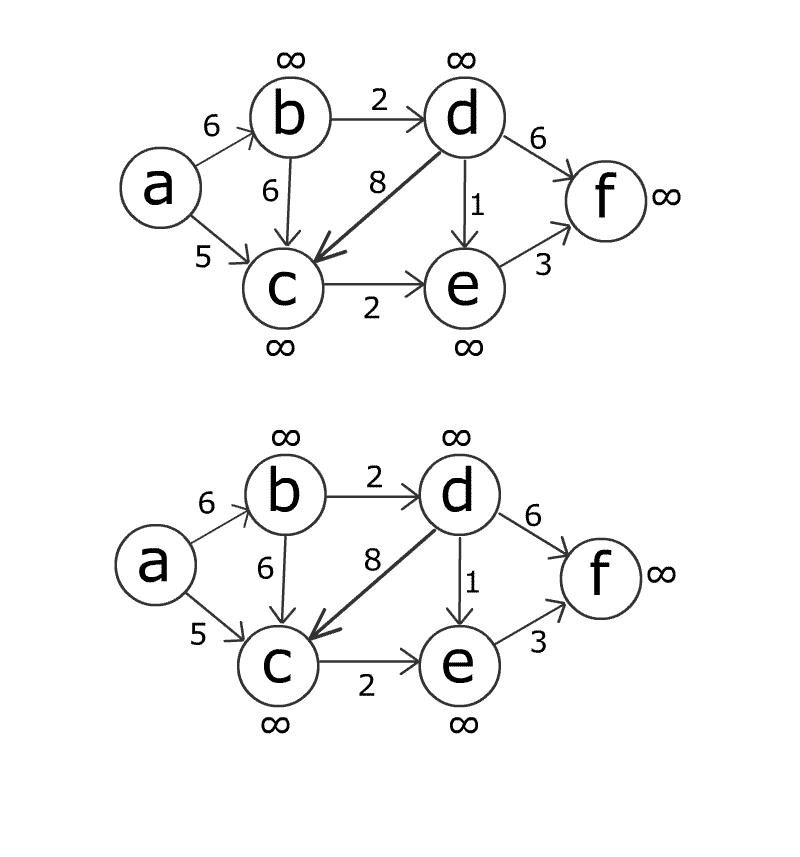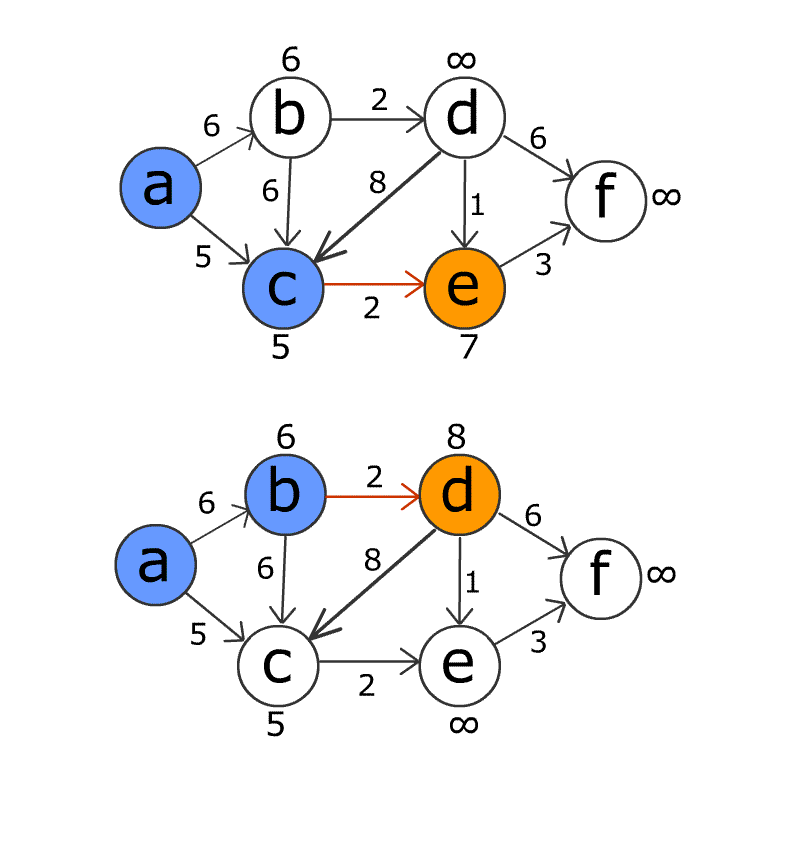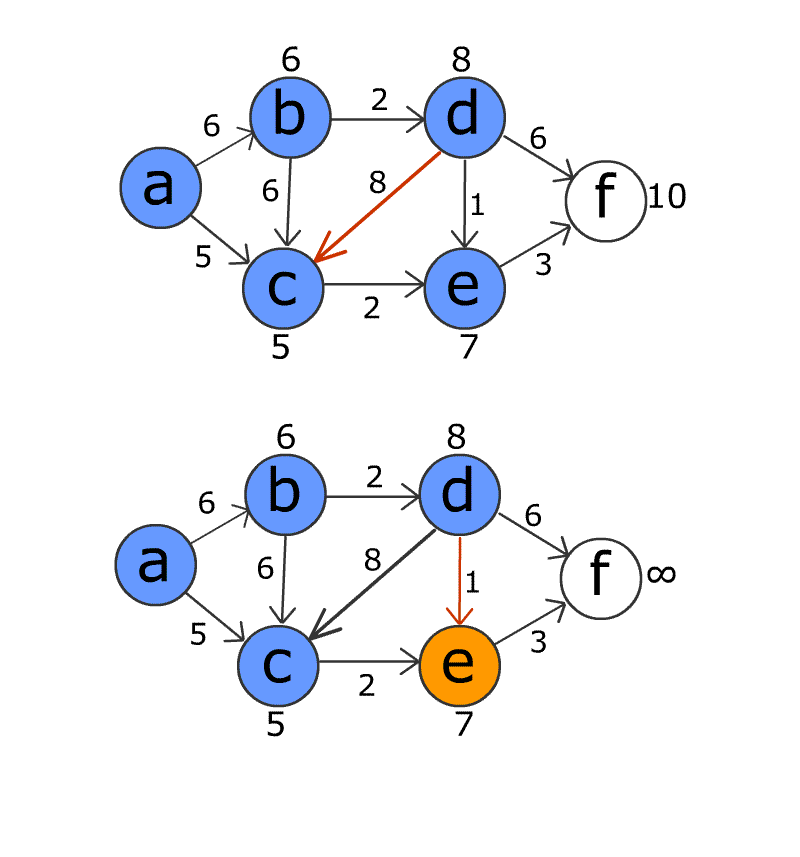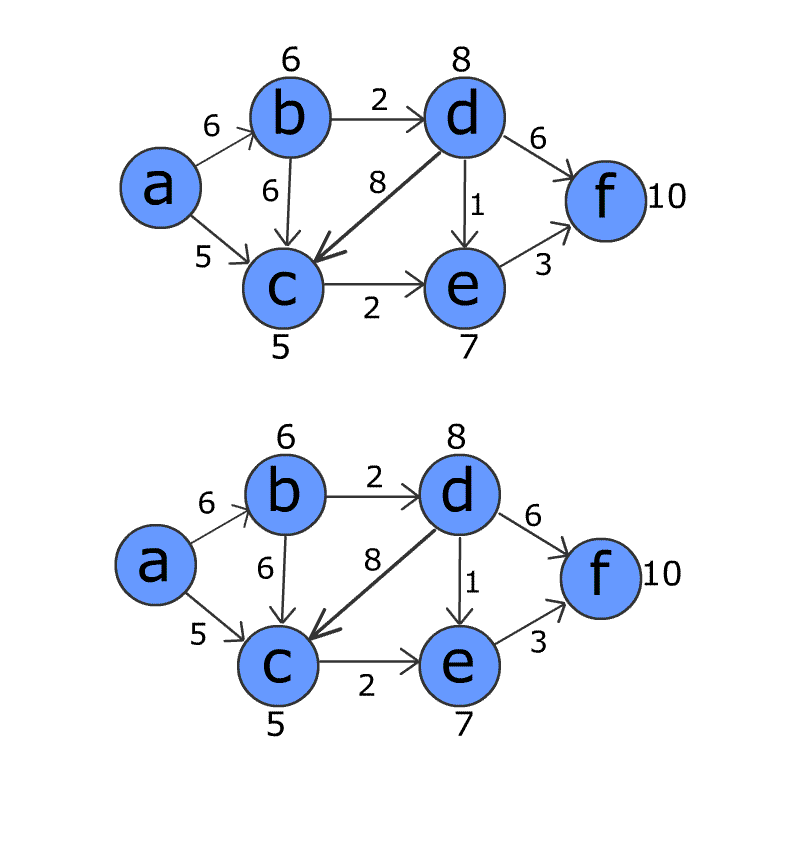
L’algoritmo di Bellman-Ford è un algoritmo utilizzato per risolvere il problema del percorso più breve in un graph pesato. Il problema del percorso più breve è il problema di trovare il percorso più breve da un punto di partenza a una destinazione. L’algoritmo di Bellman-Ford trova il percorso più breve esaminando tutte le possibili combinazioni di percorsi. Questo algoritmo può anche gestire situazioni come grafici con bordi pesati negativamente, quindi ha un uso più generale a differenza dell’algoritmo di Dijkstra.

Il principio di funzionamento dell’algoritmo di Bellman-Ford è il seguente:

1. Impostare le distanze dal punto iniziale come infinito e la distanza da se stesso come 0.
2. Rivedere tutti i bordi e gli spessori e aggiornare la distanza di un percorso dal punto iniziale al punto di destinazione per ciascun bordo.
3. Ripetere questa operazione per il numero totale di nodi - 1 volta. Il motivo per cui viene eseguito N volte è il fatto che il percorso più breve può passare attraverso al massimo N-1 spigoli. Se i percorsi più brevi possono ancora essere aggiornati dopo n volte, ciò indica che il grafico ha un loop pesato negativamente.

Algoritmo di Dijkstra è un algoritmo veloce per trovare il percorso più breve su grafi o spigoli. Ad ogni passaggio, viene selezionato e opera il nodo con la distanza minore. D’altra parte, l’algoritmo di Bellman-Ford può essere utilizzato su grafici e archi pesati negativi o positivi e ha un uso più generale. Trova il percorso più breve passando attraverso tutti i bordi e i pesi passo dopo passo, ma potrebbe richiedere più tempo poiché esamina tutti i bordi a ogni passaggio. Pertanto, mentre Dijkstra generalmente funziona più velocemente, l’algoritmo di Bellman-Ford può gestire una gamma più ampia di problemi e può anche gestire grafici o bordi pesati negativamente.

Complessità

• Worst-case performance O(|V||E|)
• Best-case performance O(|E|)
• Worst-case space complexity O(|V|)

Implementazione dell’algoritmo Bellman-Ford in GoLang:

package main

import (
	"fmt"
	"math"
)

type Edge struct {
	Source int
	Target int
	Weight int
}

func BellmanFord(edges []Edge, vertexCount int, start int) ([]int, []int) {
	distances := make([]int, vertexCount)
	predecessors := make([]int, vertexCount)

	for i := range distances {
		distances[i] = math.MaxInt32
	}
	distances[start] = 0

	for i := 1; i < vertexCount; i++ {
		for _, edge := range edges {
			if distances[edge.Source]+edge.Weight < distances[edge.Target] {
				distances[edge.Target] = distances[edge.Source] + edge.Weight
				predecessors[edge.Target] = edge.Source
			}
		}
	}

	for _, edge := range edges {
		if distances[edge.Source]+edge.Weight < distances[edge.Target] {
			fmt.Println("Negative cycle detected. Bellman-Ford algorithm cannot be applied.")
			return nil, nil
		}
	}

	return distances, predecessors
}

func main() {
	vertexCount := 5
	edges := []Edge{
		{0, 1, 2},
		{0, 2, 4},
		{1, 2, 1},
		{1, 3, 7},
		{2, 4, 3},
		{3, 4, 1},
	}

	startNode := 0
	distances, predecessors := BellmanFord(edges, vertexCount, startNode)

	if distances != nil {
		fmt.Println("Shortest distances from node", startNode)
		for i, distance := range distances {
			fmt.Printf("Node %d: Distance %d, Path: ", i, distance)
			path := []int{}
			for at := i; at != startNode; at = predecessors[at] {
				path = append([]int{at}, path...)
			}
			path = append([]int{startNode}, path...)
			fmt.Println(path)
		}
	}
}

Quando il programma viene eseguito, l’output sarà il seguente.

Shortest distances from node 0
Node 0: Distance 0, Path: [0]
Node 1: Distance 2, Path: [0 1]
Node 2: Distance 3, Path: [0 1 2]
Node 3: Distance 9, Path: [0 1 2 4 3]
Node 4: Distance 6, Path: [0 1 2 4]

È possibile accedere alla versione in esecuzione del programma da qui.

Risorse

• https://en.wikipedia.org/wiki/Bellman%E2%80%93Ford_algorithm
• https://www.baeldung.com/cs/bellman-ford