Алгоритм Беллмана-Форда
12 августа 2023 г. • ☕️ 4 мин чтение • 🏷 компьютер, программное, алгоритм, графе
Алгоритм Беллмана-Форда — это алгоритм, используемый для решения задачи поиска кратчайшего пути во взвешенном графе. Задача о кратчайшем пути — это задача о нахождении кратчайшего пути из начальной точки в конечную. Алгоритм Беллмана-Форда находит кратчайший путь, исследуя все возможные комбинации путей. Этот алгоритм также может обрабатывать такие ситуации, как графы с ребрами с отрицательным весом, поэтому он имеет более общее применение, в отличие от алгоритма Дейкстры.
Принцип работы алгоритма Беллмана-Форда следующий:
- Установите расстояния до начальной точки как бесконечность и расстояние до себя как 0.
- Просмотрите все ребра и веса и обновите расстояние пути от начальной точки до конечной точки для каждого ребра.
- Повторить эту операцию для общего количества узлов - 1 раз. Причина, по которой это делается N раз, заключается в том, что кратчайший путь может проходить не более чем через N-1 ребер. Если более короткие пути все еще могут быть обновлены после n раз, это указывает на то, что граф имеет петлю с отрицательным весом.
Алгоритм Дейкстры — это быстродействующий алгоритм поиска кратчайшего пути на положительно взвешенных графиках или края. На каждом шаге выбирается и работает узел с наименьшим расстоянием. С другой стороны, алгоритм Беллмана-Форда можно использовать с отрицательными или положительными взвешенными графами и ребрами, и он имеет более общее применение. Он находит кратчайший путь, шаг за шагом проходя все ребра и веса, но может потребоваться больше времени, так как он проверяет все ребра на каждом шаге. Таким образом, хотя алгоритм Дейкстры обычно работает быстрее, алгоритм Беллмана-Форда может решать более широкий круг задач, а также обрабатывать графы или ребра с отрицательным весом.
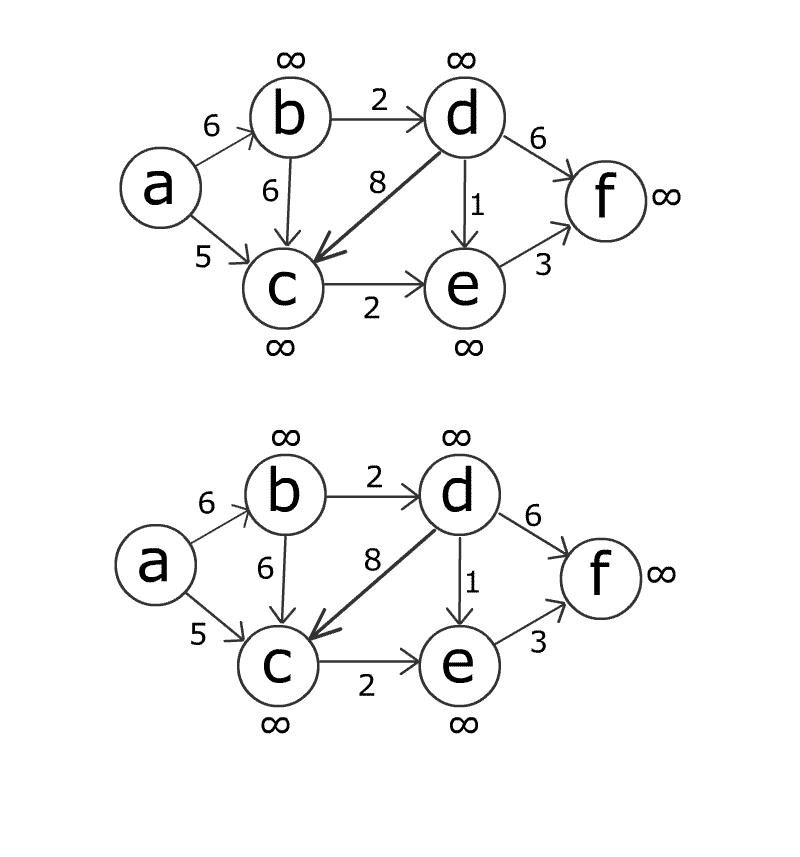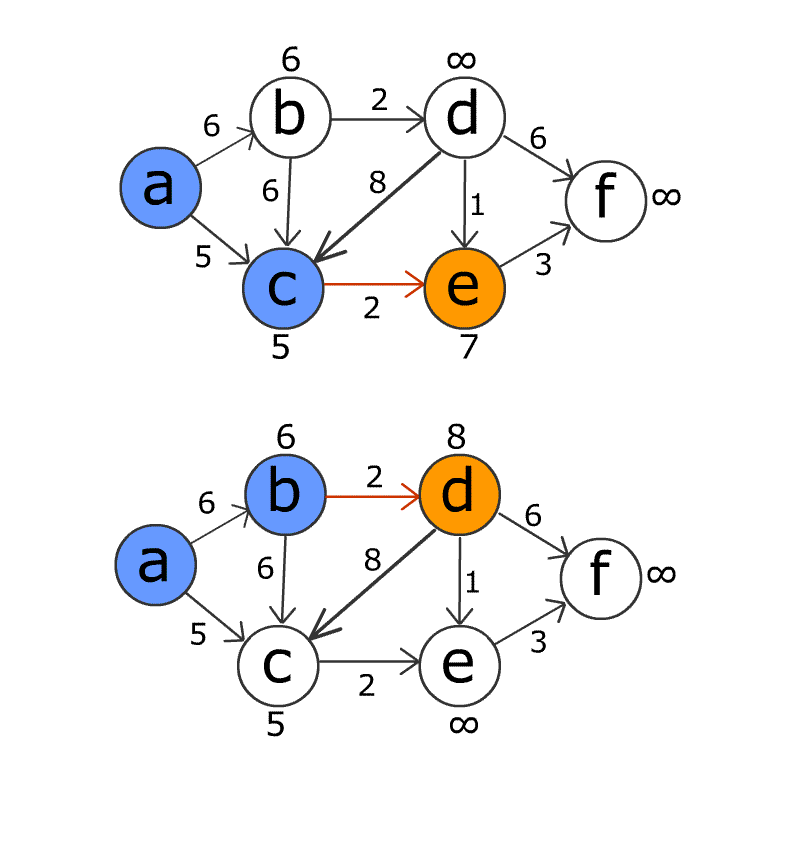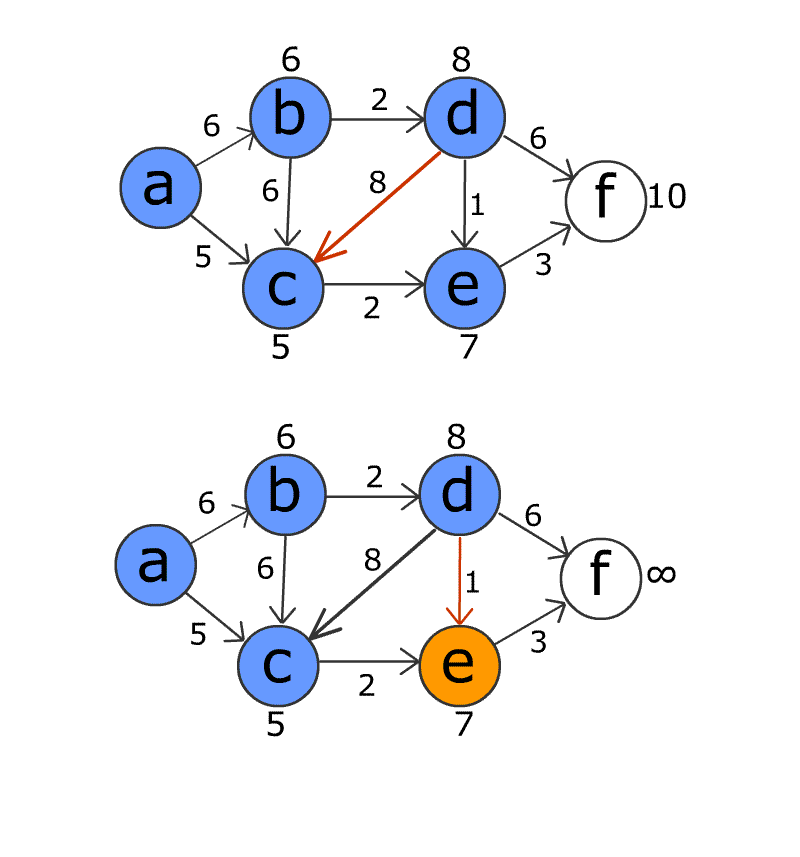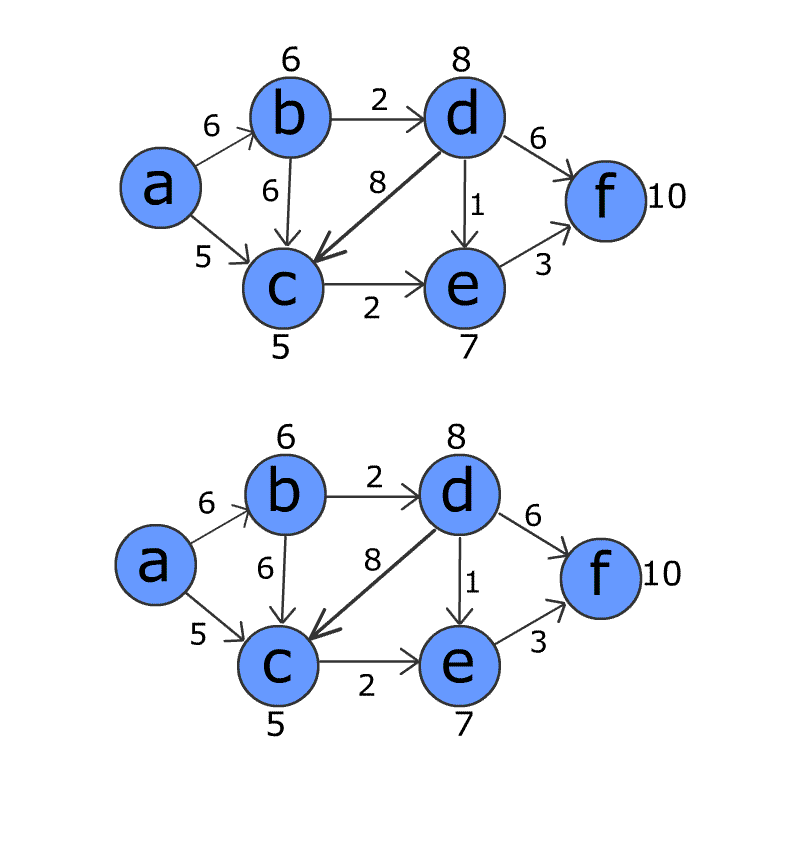
Сложность
- Worst-case performance
O(|V||E|) - Best-case performance
O(|E|) - Worst-case space complexity
O(|V|)
Реализация алгоритма Беллмана-Форда в GoLang:
package main
import (
"fmt"
"math"
)
type Edge struct {
Source int
Target int
Weight int
}
func BellmanFord(edges []Edge, vertexCount int, start int) ([]int, []int) {
distances := make([]int, vertexCount)
predecessors := make([]int, vertexCount)
for i := range distances {
distances[i] = math.MaxInt32
}
distances[start] = 0
for i := 1; i < vertexCount; i++ {
for _, edge := range edges {
if distances[edge.Source]+edge.Weight < distances[edge.Target] {
distances[edge.Target] = distances[edge.Source] + edge.Weight
predecessors[edge.Target] = edge.Source
}
}
}
for _, edge := range edges {
if distances[edge.Source]+edge.Weight < distances[edge.Target] {
fmt.Println("Negative cycle detected. Bellman-Ford algorithm cannot be applied.")
return nil, nil
}
}
return distances, predecessors
}
func main() {
vertexCount := 5
edges := []Edge{
{0, 1, 2},
{0, 2, 4},
{1, 2, 1},
{1, 3, 7},
{2, 4, 3},
{3, 4, 1},
}
startNode := 0
distances, predecessors := BellmanFord(edges, vertexCount, startNode)
if distances != nil {
fmt.Println("Shortest distances from node", startNode)
for i, distance := range distances {
fmt.Printf("Node %d: Distance %d, Path: ", i, distance)
path := []int{}
for at := i; at != startNode; at = predecessors[at] {
path = append([]int{at}, path...)
}
path = append([]int{startNode}, path...)
fmt.Println(path)
}
}
}Когда программа будет запущена, вывод будет следующим.
Shortest distances from node 0
Node 0: Distance 0, Path: [0]
Node 1: Distance 2, Path: [0 1]
Node 2: Distance 3, Path: [0 1 2]
Node 3: Distance 9, Path: [0 1 2 4 3]
Node 4: Distance 6, Path: [0 1 2 4]Доступ к рабочей версии программы можно получить по адресу [здесь] (https://go.dev/play/p/AOP-cHA1oin).
Ресурсы
- https://en.wikipedia.org/wiki/Bellman%E2%80%93Ford_algorithm
- https://www.baeldung.com/cs/bellman-ford