Distributed systems are one of the most critical technological building blocks of our day. In databases, blockchain networks, multi-layered enterprise software architectures, cloud computing infrastructures and many other areas, we use systems based on the principle of different physical or virtual nodes working together. However, many problems such as communication failures, hardware failures, malicious attacks or software errors can occur in these systems. These problems directly affect the overall operation and reliability of the distributed system.

One of the most important questions that need to be answered in the design of a distributed system is “How can the system work properly even if some of the system components fail or are intentionally malicious?” The most classic and striking example of this problem is the problem definition put forward by Leslie Lamport, Robert Shostak and Marshall Pease in 1982 and referred to in the literature as the “Byzantine Generals Problem”.

What is the Byzantine Generals Problem?

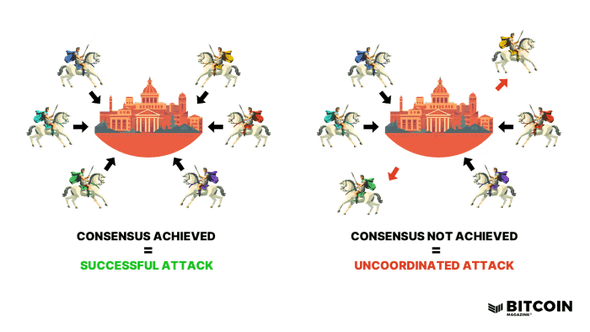
The Byzantine Generals Problem is presented through a metaphorical story that essentially describes the difficulty of reaching consensus in a distributed system with unreliable communication channels and potentially malicious participants. The main idea of ​​the problem can be summarized as follows:

1. There are generals commanding different army units in the Byzantine Empire.
2. These generals are positioned in different locations and must make a strategic decision such as attacking or retreating to a common target (e.g. a castle).
3. The decision of the generals to attack or retreat must be joint; if some attack and others retreat, the army will fall apart and a major defeat will occur.
4. The generals can only communicate with each other through a messenger (a messenger carrying a message).
5. The messenger can be caught on the way and change the message, or any general can deliberately spread false information (may be malicious).

In this scenario, the question “Can each general reach the same conclusion by learning the majority decision correctly?” is the main issue to be solved. If there is one or more rogue/malicious generals in the system, they may try to prevent the system from reaching consensus by sending false messages. The Byzantine Generals Problem represents the question of “how can we get the correct (honest) nodes in the system to reach a consensus against any number of faulty or malicious nodes?”

History and Importance of the Problem

The Byzantine Generals Problem was first described in detail in 1982 by Leslie Lamport, Robert Shostak and Marshall Pease in the article “The Byzantine Generals Problem”. It is a turning point in the field of distributed systems and fault tolerance. Until then, “fault tolerance” mostly focused on the question of “what happens if a node crashes?” (for example, if a server suddenly shuts down). However, a new perspective was needed to address more complex forms of error, including malicious behavior. This problem is especially important at the following critical points:

• Secure Distributed Computing: Security and correctness are essential in environments such as financial systems, military systems, and critical infrastructures.
• Blockchain Technology: In blockchains such as Bitcoin, it is uncertain whether the network participants (miners, validators) are honest. Ensuring Byzantine fault tolerance is a fundamental requirement for the continuity of blockchains.
• Cloud Computing and Microservices Architecture: In cloud environments where many different servers and services communicate with each other, some of the nodes in question may experience network or software problems.
• Distributed Databases: Nodes with different replicas on a database cluster must produce a correct majority decision (consensus).

Types of Errors and Byzantine Errors

We can roughly divide the possible types of errors in distributed systems into two:

1. Crash or Passive Errors: A node stops working completely, does not send messages or responds. All other honest nodes can develop a strategy by saying “This node is null and void, let’s ignore it”.
2. Byzantine (Active and Malicious) Errors: Instead of stopping working, the node exhibits malicious behavior (changing messages, sending contradictory messages, duplicating messages unnecessarily, etc.) or unexpected failures (sending wrong data as a result of incorrect calculation, deliberately sabotaging the communication channel, etc.).

Byzantine errors are much more dangerous than classic crash errors. Because the malicious or faulty node does not have to remain fixed in only one behavior; it can try various methods to deliberately harm the operation of the system. This requires extremely complex precautions to be taken when designing consensus protocols.

Formal Definition of the Byzantine Generals Problem

Let’s make the problem a bit more formal:

• Let’s say there are 𝑛 nodes in the system.
• Some of these nodes may exhibit Byzantine behavior (malicious, faulty, inconsistent, etc.).
• Each node starts with a specific message value (e.g. “Attack”, “Don’t Attack”, or “0”/“1”).
• The goal is for all honest nodes to agree on the same common value (e.g. “Attack”), if possible.
• While honest nodes stick to the protocol, Byzantine nodes can act without following any rules.

How will this agreement be achieved, especially when at least 𝑓 of the 𝑛 nodes can be Byzantine (malicious)? The solution conditions of the problem must meet the following conditions:

1. Integrity: If the decision message of an honest node is 𝑣, all other honest nodes must agree on 𝑣.
2. Consensus: The output (decision) of all honest nodes is the same.
3. Validity: If there is a valid message value in the input, the system must make a decision without deviating from this message value. (For example, if there are no malicious nodes, all honest nodes must be able to reach a consensus on their own inputs.)

It has been theoretically proven that at least 3f+1 nodes are required to provide 𝑓 Byzantine fault tolerance in a synchronous network. This is a basic reference point for the design of many consensus protocols.

Fault Tolerance in Distributed Systems

We can better understand the concept of fault tolerance in distributed systems by starting from the Byzantine Generals Problem. Fault tolerance refers to the ability of the system to produce generally correct results even if a part of the system fails or is deliberately sabotaged.

Requirements

• Redundancy: Distributed systems distribute the same task to multiple nodes to avoid a single point of failure. Thus, if a node crashes or lies, other honest nodes can protect the correct information.
• Secure Communication Channels: Techniques such as cryptographic methods, message integrity and authentication make it difficult to manipulate messages.
• Consensus Protocol: Nodes must reach a common decision by majority vote or other mathematical mechanisms.

Crash Fault Tolerance vs. Byzantine Fault Tolerance

• Crash Fault Tolerance (CFT): Only handles the case where nodes crash and do not send messages (or send delayed messages).
• Byzantine Fault Tolerance (BFT): Handles the case where nodes may intentionally send misleading or inconsistent messages. Therefore, BFT mechanisms are more complex and costly than CFT.

Approaches to Achieving Byzantine Fault Tolerance

1. Classical Algorithms

In the Byzantine Generals Problem paper, algorithms that reach consensus in a certain number of communication rounds under a synchronous model, with the condition n≥3f+1, are proposed. However, these algorithms can be very costly in practice (in terms of network traffic and computational load).

For example, the original “Oral Message” (OM) and “Signed Message” (SM) protocols include distributed copies of messages, signatures, verifier lists, etc. to limit the impact of faulty nodes (generals). At each step, messages are replicated and distributed, thus creating a global belief.

2. Practical Byzantine Fault Tolerance (PBFT)

The PBFT (Practical Byzantine Fault Tolerance) protocol, proposed by Miguel Castro and Barbara Liskov in 1999, had a huge impact in the world of distributed systems. Because PBFT was partly aimed at being a “practical” solution; that is, it aimed to develop a protocol that would work with low latency in a realistic network model (partly synchronous).

• Operation Summary: *Client sends a request (for example, a transaction, a data update) to the system. *Primary Node receives the request and distributes it to other replicas. *Replicas perform a “pre-prepare” and “prepare” phase to ensure that the request sent by the leader is valid, and a kind of consensus (majority) is achieved. *When a sufficient majority is reached, the “commit” phase is passed and the transaction is verified. *The result is returned to the client.
• Byzantine Fault Tolerance: PBFT tolerates at most 𝑓 Byzantine faults out of the total number of nodes 𝑛. For this protocol, the condition n≥3f+1 is also required.

PBFT and its derivatives are currently used in many permissioned blockchains, enterprise data sharing systems, and other applications where fault tolerance is critical.

3. Raft, Paxos and BFT Variants

• Paxos and Raft are actually consensus protocols that are resistant to collapse faults (CFT). In other words, they do not provide direct security against Byzantine faults. However, approaches such as BFT-Paxos have emerged with different additions and strengthened versions.
• Tendermint (a blockchain consensus mechanism) provides speed and high verification guarantees by using a BFT approach similar to PBFT.
• New generation protocols such as Honey Badger BFT focus on providing BFT consensus even in partially synchronous or asynchronous networks.

Examples and Application Areas

1. Blockchains

• Bitcoin: It does not use PBFT directly, instead it tries to provide a kind of “economic” BFT based on the Proof-of-Work (PoW) mechanism. If attackers gain 51% mining power, they can manipulate the network.
• Ethereum: It was initially based on PoW, but with the Ethereum 2.0 transition, it has turned to Proof-of-Stake (PoS) and protocols such as Casper, which include BFT principles.
• Hyperledger Fabric: It is a permissioned blockchain platform and enables consensus mechanisms with Byzantine fault tolerance such as PBFT.

2. Distributed Databases and Enterprise Systems

Large enterprise data centers use different replication strategies to provide high availability and consistency. While some are content with crash fault tolerance, BFT solutions can be preferred in environments where security is critical (e.g. finance, defense, healthcare).

• For example, Google Spanner is a CFT-based system, but it requires very high accuracy and continuity. When necessary, Byzantine behaviors can also be partially prevented with cryptographic signature and data integrity verification techniques.

3. Military and Space Applications

• Institutions such as NASA care about the ability of different components in the control systems of spacecraft and rockets to work independently and verify data. For example, in a very critical system, the same sensor data is processed by different computers and a kind of voting mechanism (the same Paxos or PBFT-like approach) can be run between them.
• In military environments, fake commands or false intelligence information sent by the enemy are similar to Byzantine errors. Therefore, ensuring the integrity of data in centralized chains of command is a reflection of this problem in real life.

4. IoT (Internet of Things)

In networks of IoT devices such as smart cities, health sensors, and production lines, it is possible that some of the devices may be attacked or malfunction. Some IoT platforms require lightweight BFT mechanisms.

A Detailed Scenario Example

In this scenario, let’s consider a smart traffic light system in a city:

1. Nodes: Control units (traffic lights) at different intersections of the city, central management servers, and regional management devices.
2. Need for Consensus: A certain green light duration decision needs to be made to balance traffic congestion at certain hours. For example, green light durations between intersections should be synchronized to optimize traffic flow.

3. Possible Byzantine Error:

   • A traffic light control unit reports incorrectly or does not send any data at all.
   • A malicious attacker manipulates real data by modifying packets in the network.
   • A management device intentionally sends conflicting instructions to different intersections.

4. Solution Approach:

   • Each control unit sends sensor data to all other units (or a subset of the majority) along with a digital signature.
   • A PBFT-like algorithm collects this data and determines the next signaling time with a “majority decision”.
   • If inconsistent data comes from some units or servers, it is detected by the majority (signature tracking, data validity check) and ignored.
   • As a result, despite a unit being attacked or malfunctioning, the entire system can make the correct adjustment.

This scenario, although complex, can be shown as an example of a typical Byzantine fault tolerance problem that we may encounter in large-scale IoT projects or smart traffic systems in real life.

A Simple “Byzantine” Example with Golang

The following code contains the following components:

• Node: Each node has an ID, a “proposal” (e.g. “Attack” or “Retreat”), a “Byzantine” status, and a thread where it stores incoming messages.
• Broadcast: Nodes send messages to each other. A Byzantine node can send manipulated or different messages based on the incoming request.
• Consensus: In its simplest form, each honest node updates its decision by considering the majority of the messages it receives.

Important Note: This code example is not a “full” implementation of a real PBFT or BFT algorithm. The purpose is to present a mini-scenario to illustrate the concepts and potential manipulations. In a production environment, much more complex structures such as cryptographic signatures, communication protocols, timeout mechanisms, error detection are required.

package main

import (
    "fmt"
    "math/rand"
    "time"
)

// Message represents a simple structure that one node sends to another node.
type Message struct {
    From    int    // ID of the sender
    Content string // Proposal ("Attack" or "Retreat")
}

// Node represents a general (node) in the system.
type Node struct {
    ID            int
    Proposal      string   // This node's initial proposal
    IsByzantine   bool     // Is this node malicious?
    ReceivedMsgs  []Message
    FinalDecision string   // Final decision after consensus
}

// Broadcast allows each node to send messages to other nodes.
// Byzantine behavior is simplified to "manipulate the message" here.
func (n *Node) Broadcast(nodes []*Node) {
    for _, other := range nodes {
        if other.ID == n.ID {
            continue // Skip sending a message to itself
        }

        // The message content to be sent
        msgContent := n.Proposal

        // If this node is Byzantine, it may manipulate the message
        if n.IsByzantine {
            // For example, with a random probability, flip the message
            // (Attack -> Retreat, Retreat -> Attack)
            if rand.Float64() < 0.5 {
                if msgContent == "Attack" {
                    msgContent = "Retreat"
                } else {
                    msgContent = "Attack"
                }
            }
        }

        // "Send" the message to the other node
        other.Receive(Message{
            From:    n.ID,
            Content: msgContent,
        })
    }
}

// Receive stores incoming messages from other nodes.
func (n *Node) Receive(msg Message) {
    n.ReceivedMsgs = append(n.ReceivedMsgs, msg)
}

// Decide makes a final decision based on all received messages.
// It simply checks which proposal is in the majority (Attack or Retreat)
// and updates its own decision accordingly.
func (n *Node) Decide() {
    attackCount := 0
    retreatCount := 0

    for _, msg := range n.ReceivedMsgs {
        if msg.Content == "Attack" {
            attackCount++
        } else if msg.Content == "Retreat" {
            retreatCount++
        }
    }

    // Also consider the node's own initial proposal in the count
    if n.Proposal == "Attack" {
        attackCount++
    } else {
        retreatCount++
    }

    // The final decision is assigned based on the majority
    if attackCount > retreatCount {
        n.FinalDecision = "Attack"
    } else if retreatCount > attackCount {
        n.FinalDecision = "Retreat"
    } else {
        // In case of a tie, keep its original proposal
        n.FinalDecision = n.Proposal
    }
}

// NewNode is a helper function to create a new Node.
func NewNode(id int, proposal string, isByzantine bool) *Node {
    return &Node{
        ID:          id,
        Proposal:    proposal,
        IsByzantine: isByzantine,
    }
}

func main() {
    rand.Seed(time.Now().UnixNano())

    // Example scenario:
    // Let's create a total of 5 nodes. One of them will be Byzantine.
    // Each node will initially propose either "Attack" or "Retreat".
    nodes := []*Node{
        NewNode(0, "Attack",  false),
        NewNode(1, "Attack",  false),
        NewNode(2, "Retreat", false),
        NewNode(3, "Attack",  true),  // Malicious (Byzantine)
        NewNode(4, "Retreat", false),
    }

    // Round 1: Each node broadcasts its current proposal to others
    for _, node := range nodes {
        node.Broadcast(nodes)
    }

    // Round 2 (Optional): If you want multiple rounds, you could
    // update each node’s Proposal based on received messages
    // and broadcast again. In this simple example, we do just one round.

    // Now each node decides based on the messages it received
    for _, node := range nodes {
        node.Decide()
    }

    // Print results
    fmt.Println("=== Final Decisions ===")
    for _, node := range nodes {
        fmt.Printf("Node %d [Byzantine=%v] | Initial Proposal: %s | Final Decision: %s\n",
            node.ID, node.IsByzantine, node.Proposal, node.FinalDecision)
    }
}

When the program is run, the output will be as follows.

=== Final Decisions ===
Node 0 [Byzantine=false] | Initial Proposal: Attack  | Final Decision: Attack
Node 1 [Byzantine=false] | Initial Proposal: Attack  | Final Decision: Attack
Node 2 [Byzantine=false] | Initial Proposal: Retreat | Final Decision: Attack
Node 3 [Byzantine=true]  | Initial Proposal: Attack  | Final Decision: Retreat
Node 4 [Byzantine=false] | Initial Proposal: Retreat | Final Decision: Attack

Here, 3 out of 5 nodes’ final decision is “Attack”, 1 is “Retreat”; even the Byzantine node itself may have been influenced by the majority of incoming messages (and the messages it manipulated) and reached the opposite conclusion.

The working version of the program can be accessed here.

Note: In a real BFT protocol, signatures and consistent broadcast mechanisms are used to prevent (or catch) nodes from sending different messages to different nodes. Here, we added a partial manipulation to the “same message to all” assumption to simply illustrate the point.

Performance and Cost

Protecting against Byzantine errors always means additional computational, communication, and management costs. Protocols may require multiple rounds of message exchanges to confirm a transaction. Additionally, cryptographic operations such as signature verification add overhead. Therefore, designers consider the following questions based on the requirements of the system:

• How many nodes will be running?
• What is the expected attack or failure rate?
• Is it a real-time system, how much latency is tolerated?
• Are hardware resources and bandwidth sufficient?

It can still be challenging to provide BFT on large nodes (e.g. hundreds, thousands). Therefore, in practice, BFT protocols are more common in smaller, permissioned networks (consortium blockchains, enterprise data centers, etc.).

Future Trends

In our age where distributed systems are becoming more and more important every day, the Byzantine Generals Problem and BFT protocols will continue to play a critical role in the future. Intensive research and development studies are ongoing, especially in the following areas:

1. Asynchronous BFT Protocols: It is even more difficult to provide BFT in completely asynchronous networks (no delay limit, message order is ambiguous). New approaches such as Honey Badger BFT stand out in this regard.
2. Zero-Knowledge and Cryptographic Developments: Privacy-focused BFT protocols are being developed where nodes will contribute to verification without disclosing data.
3. Quantum-Resistant Signature Schemes: In the future, with the development of quantum computers, there is a possibility that existing cryptographic signature schemes will become breakable. BFT protocols may also require quantum-resistant signature methods.
4. Energy Efficiency and Green Computing: Blockchain and distributed consensus protocols are criticized for their high energy consumption. More efficient BFT mechanisms and Proof-of-Stake style protocols continue to be developed.

The Byzantine Generals Problem is a fundamental reference for fault tolerance in distributed systems and especially for precautions to be taken against malicious or faulty nodes. Thanks to this problem, system designers and researchers have worked on protocols that can work correctly despite the “worst” scenarios, and powerful solutions such as PBFT, Tendermint, Honey Badger BFT have emerged.

From today’s blockchain technologies to corporate data centers, from IoT networks to military systems, there are situations in which “a large number of nodes must make the right decision at the same time”. At this point, the Byzantine Generals Problem continues to be one of the most important guides that provide answers to the question of “how to achieve distributed consensus?” in theoretical and practical terms.

In summary, achieving Byzantine fault tolerance in distributed systems is not easy; it requires additional cost, complexity, and meticulous protocol design. However, the gain (high security, accuracy, uninterrupted operation) obtained when these difficulties are overcome is indispensable in critical projects. Therefore, closely following the development of the Byzantine Generals Problem and BFT protocols in the coming years will play a key role in shaping the future of distributed systems.

Resources

• https://en.wikipedia.org/wiki/Byzantine_fault
• https://lamport.azurewebsites.net/pubs/byz.pdf
• https://pmg.csail.mit.edu/papers/osdi99.pdf
• https://bitcoin.org/bitcoin.pdf
• https://bitcoinmagazine.com/glossary/what-is-the-byzantine-generals-problem