Sıralama algoritmaları, bilgisayar bilimlerinin temel taşlarından birini oluşturur. Bilgisayarlar verilerle çalışırken, bu verileri düzenlemek ve sıralamak sıklıkla karşılaşılan bir gerekliliktir. Bu nedenle, sıralama algoritmaları bilgisayar bilimleri ve yazılım geliştirmenin vazgeçilmez bir parçasıdır. Veri sıralamasının birçok farklı alanda kullanıldığına tanık olabiliriz, örneğin veri tabanlarındaki kayıtların sıralanması, arama motorlarının sonuçlarının sıralanması, grafiklerin çizdirilmesi sırasında verilerin düzenlenmesi gibi birçok uygulama bu temel işlemi gerektirir. Bu yüzden bilim insanları ve yazılım geliştiricileri, veri sıralama işlemi için en verimli ve etkili yöntemleri geliştirmeye ve optimize etmeye çalışırlar. Bu amaçla birçok farklı sıralama algoritması tasarlanmış ve incelenmiştir.

Heap Sort Nedir?

Heap Sort, veri sıralama işlemi için kullanılan bir karşılaştırmalı sıralama algoritmasıdır. Bu algoritma, veriyi bir ağaç yapısı olan bir “heap” (yığın) kullanarak sıralar. Heap, bir ağaç yapısı olup her düğümün iki alt düğümü vardır. Bununla birlikte, Heap Sort’ta kullanılan heap, “maksimum heap” veya “minimum heap” olarak adlandırılır ve belirli bir özelliği korur: Her düğümün üst düğümden daha büyük (maksimum heap) veya daha küçük (minimum heap) olması gerekir.

Heap Sort, bu maksimum veya minimum heap yapısını kullanarak sıralama işlemini gerçekleştirir. İşlem sırasında, heap yapısı verilerin yeniden düzenlenmesi için kullanılır ve sonuç olarak sıralanmış bir veri dizisi elde edilir.

Heap Sort Nasıl Çalışır?

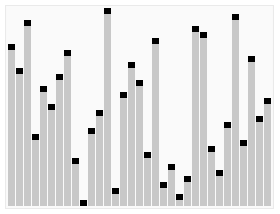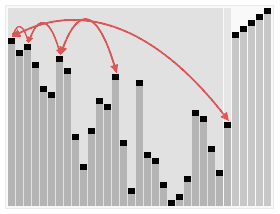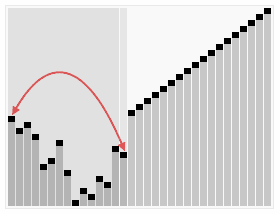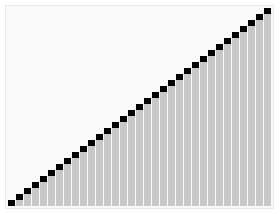
Heap Sort algoritması aşağıdaki adımları izler:

1. Başlangıçta Max Heap Oluşturma: İlk adım, veri dizisini bir maksimum heap yapısı haline getirmektir. Bu, diziyi baştan sona dolaşarak heap özelliğini sağlamak için “heapify” adı verilen bir işlemi içerir. Bu işlem, her düğümün üst düğümden daha büyük olduğundan emin olur.
2. Kök Düğümü ile Son Elemanı Değiştirme: Maksimum heap yapısının oluşturulmasının ardından, kök düğümü (en büyük eleman) ile son elemanın yerini değiştirilir. Bu, en büyük elemanın sıralanan bölümün sonuna taşınması anlamına gelir.
3. Heap Boyutunu Azaltma: Veri dizisinin sonundaki eleman artık sıralanmıştır, bu nedenle heap boyutunu bir azaltırız. Yani heap yapısının son elemanını çıkarırız.
4. Heapify İşlemi: Kök düğümünü tekrar heap özelliğini sağlayacak şekilde düzenlemek için “heapify” işlemi yapılır.
5. Tekrarlama: Adımlar 2-4, heap yapısı tamamen boşalana kadar tekrarlanır. Bu, veri dizisi tamamen sıralanana kadar devam eder.
6. Sonuç: Heap yapısı tamamen boşaldığında, veri dizisi sıralanmış olur ve işlem tamamlanır.

Aşağıda, Heap Sort algoritmasının basit bir pseudocode örneği verilmiştir:

procedure heapSort(arr):
    n = length(arr)

    for i from n/2 down to 1:
        heapify(arr, n, i)

    for i from n down to 2:
        swap(arr[1], arr[i])
        heapify(arr, i-1, 1)

procedure heapify(arr, n, i):
    largest = i
    leftChild = 2 * i
    rightChild = 2 * i + 1

    if leftChild <= n and arr[leftChild] > arr[largest]:
        largest = leftChild

    if rightChild <= n and arr[rightChild] > arr[largest]:
        largest = rightChild

    if largest != i:
        swap(arr[i], arr[largest])
        heapify(arr, n, largest)

Heap Sort’un Zaman ve Alan Karmaşıklığı

Heap Sort, en kötü durumda O(n log n) zaman karmaşıklığına sahiptir. Ayrıca, ekstra bir bellek gerektirmez, bu nedenle O(1) ekstra bellek karmaşıklığına sahiptir. Bu özellikleri nedeniyle Heap Sort, büyük veri setleri üzerinde etkili bir sıralama algoritmasıdır.

Kullanım Alanları

Heap Sort, genellikle yerleşik sıralama fonksiyonları kullanılamadığında veya sabit bellek kullanımı gerektiren uygulamalarda tercih edilir. Özellikle gömülü sistemlerde, işlemci kaynakları sınırlı olduğunda ve harici belleğin kullanılmasına izin verilmediğinde tercih edilen bir sıralama algoritmasıdır.

Heap Sort, etkili bir sıralama algoritmasıdır ve genellikle veri sıralamak için kullanılır. Max Heap yapısının kullanımı ve veri dizisinin sürekli olarak yeniden düzenlenmesi, bu algoritmanın veri sıralama işlemi için etkili bir yol olduğunu gösterir. Ancak, daha hızlı sıralama algoritmaları mevcut olduğunda ve ekstra bellek kullanımına izin verildiğinde, bu alternatifler tercih edilebilir.

Heap Sort, bilgisayar bilimlerinin temel konularından biridir ve sıralama algoritmaları hakkında daha fazla bilgi edinmek isteyenler için önemli bir başlangıç noktasıdır.

GoLang’de Heap Sort uygulaması:

package main

import "fmt"

func heapSort(arr []int) {
    n := len(arr)

    for i := n/2 - 1; i >= 0; i-- {
        heapify(arr, n, i)
    }

    for i := n - 1; i > 0; i-- {
        arr[0], arr[i] = arr[i], arr[0]
        heapify(arr, i, 0)
    }
}

func heapify(arr []int, n, i int) {
    largest := i
    leftChild := 2*i + 1
    rightChild := 2*i + 2

    if leftChild < n && arr[leftChild] > arr[largest] {
        largest = leftChild
    }

    if rightChild < n && arr[rightChild] > arr[largest] {
        largest = rightChild
    }

    if largest != i {
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)
    }
}

func main() {
    arr := []int{12, 11, 13, 5, 6, 7}
    fmt.Println("Unsorted Array:", arr)

    heapSort(arr)

    fmt.Println("Sorted Array:", arr)
}

Program çalıştırıldığında çıktısı aşağıdaki gibi olacaktır.

Unsorted Array: [12 11 13 5 6 7]
Sorted Array: [5 6 7 11 12 13]

Programın çalışır haline şuradan erişilebilir.

Kaynaklar

• https://en.wikipedia.org/wiki/Heapsort