Sorting algorithms form one of the cornerstones of computer science. When computers work with data, organizing and sorting that data is a frequent requirement. Therefore, sorting algorithms are an indispensable part of computer science and software development. We can witness that data sorting is used in many different areas, for example, many applications such as sorting records in databases, sorting the results of search engines, arranging data when drawing graphs, etc. require this basic process. That’s why scientists and software developers try to develop and optimize the most efficient and effective methods for data sorting. Many different sorting algorithms have been designed and examined for this purpose.

What is Heap Sort?

Heap Sort is a comparison sorting algorithm used for data sorting. This algorithm sorts data using a “heap”, which is a tree structure. Heap is a tree structure and each node has two child nodes. However, the heap used in Heap Sort is called “maximum heap” or “minimum heap” and retains a specific property: Each node must be larger (maximum heap) or smaller (minimum heap) than its parent node.

Heap Sort performs the sorting process using this maximum or minimum heap structure. During the process, the heap structure is used to rearrange the data, resulting in a sorted array of data.

How Does Heap Sort Work?

The Heap Sort algorithm follows the following steps:

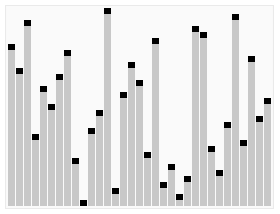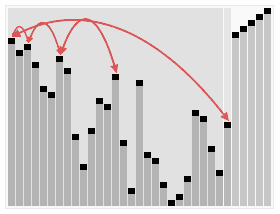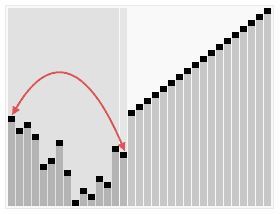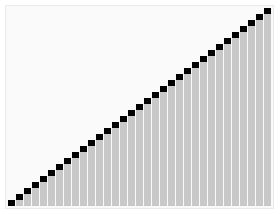
1. Creating Max Heap at Startup: The first step is to make the data array into a max heap structure. This involves an operation called “heapify” to provide the heap property by traversing the array. This process ensures that each node is larger than its parent node.
2. Changing the Root Node and the Last Element: After creating the maximum heap structure, the root node (largest element) and the last element are replaced. This means moving the largest element to the end of the sorted section.
3. Reducing Heap Size: The element at the end of the data array is now sorted, so we reduce the heap size by one. So we remove the last element of the heap structure.
4. Heapify Process: “Heapify” process is performed to rearrange the root node to provide the heap feature again.
5. Iteration: Steps 2-4 are repeated until the heap structure is completely empty. This continues until the data array is completely sorted.
6. Result: When the heap structure is completely empty, the data array is sorted and the process is completed.

Below is a simple pseudocode example of the Heap Sort algorithm:

procedure heapSort(arr):
    n = length(arr)

    for i from n/2 down to 1:
        heapify(arr, n, i)

    for i from n down to 2:
        swap(arr[1], arr[i])
        heapify(arr, i-1, 1)

procedure heapify(arr, n, i):
    largest = i
    leftChild = 2 * i
    rightChild = 2 * i + 1

    if leftChild <= n and arr[leftChild] > arr[largest]:
        largest = leftChild

    if rightChild <= n and arr[rightChild] > arr[largest]:
        largest = rightChild

    if largest != i:
        swap(arr[i], arr[largest])
        heapify(arr, n, largest)

Time and Space Complexity of Heap Sort

Heap Sort has a worst case time complexity of O(n log n). Also, it doesn’t require any extra memory, so it has O(1) extra memory complexity. Due to these features, Heap Sort is an effective sorting algorithm on large data sets.

Usage areas

Heap Sort is generally preferred when built-in sorting functions cannot be used or in applications that require constant memory usage. It is a preferred sorting algorithm, especially in embedded systems, when processor resources are limited and the use of external memory is not allowed.

Heap Sort is an efficient sorting algorithm and is often used to sort data. The use of the Max Heap structure and the constant rearrangement of the data array indicate that this algorithm is an effective way to sort data. However, when faster sorting algorithms are available and allow for extra memory usage, these alternatives may be preferred.

Heap Sort is a fundamental topic in computer science and an important starting point for those who want to learn more about sorting algorithms.

Heap Sort implementation in GoLang:

package main

import "fmt"

func heapSort(arr []int) {
    n := len(arr)

    for i := n/2 - 1; i >= 0; i-- {
        heapify(arr, n, i)
    }

    for i := n - 1; i > 0; i-- {
        arr[0], arr[i] = arr[i], arr[0]
        heapify(arr, i, 0)
    }
}

func heapify(arr []int, n, i int) {
    largest := i
    leftChild := 2*i + 1
    rightChild := 2*i + 2

    if leftChild < n && arr[leftChild] > arr[largest] {
        largest = leftChild
    }

    if rightChild < n && arr[rightChild] > arr[largest] {
        largest = rightChild
    }

    if largest != i {
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)
    }
}

func main() {
    arr := []int{12, 11, 13, 5, 6, 7}
    fmt.Println("Unsorted Array:", arr)

    heapSort(arr)

    fmt.Println("Sorted Array:", arr)
}

When the program is run, its output will be as follows.

Unsorted Array: [12 11 13 5 6 7]
Sorted Array: [5 6 7 11 12 13]

The working version of the program can be accessed from here.

Resources

• https://en.wikipedia.org/wiki/Heapsort
• https://www.interviewkickstart.com/learn/heap-sort