The Bloom Filter is a composable probability-based data structure that is often used within data structures and is particularly used to speed up data searches. This data structure is used to check the presence (existence or non-existence) of elements quickly and with low memory usage.

The Bloom Filter was introduced by Burton Howard Bloom in 1970 and works particularly effectively on large datasets. The Bloom Filter is used when the answer is “uncertain”, meaning that a particular element is likely to be found in the set, rather than stating that it is definitely or not. Therefore, the Bloom Filter, besides being fast and lightweight, can provide the probability of the response with an acceptable margin of error.

Bloom Filter is a probabilistic data structure. It is used to check if an item is in a set. This can also be achieved using other data structures. However, the Bloom filter does this efficiently.

Algorithm

An empty Bloom Filter is a string of m bits all set to 0. Also, k different hash functions must be defined, each of which maps or complicates some set element to an array position m. This creates a uniform random distribution. Usually k is a constant much smaller than m and is proportional to the number of elements added; The proportional constant of k and m is determined by the filter’s intended false positive rate.

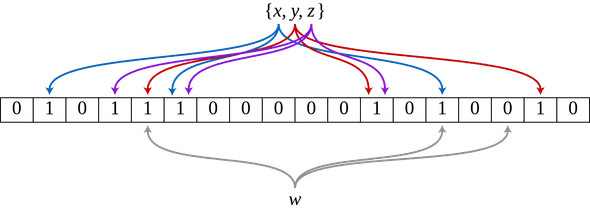
Below we can see an example of a Bloom Filter representing the set {x, y, z}. Colored arrows indicate the positions in the bit array where each set element is mapped. The W element is not in the set {x, y, z} because it is complexed to a bit-string location containing 0. For this figure, m = 18 and k = 3.

The Bloom Filter consists of a string of k-bits long and several hash functions. Here’s how it works:

• An array with k predetermined null bits is created.
• When there is an element to be added, k different hash functions are used for this element. Each hash function returns a position of the element.
• These obtained positions are marked to the corresponding positions in the bit string (given a value of 1).
• When we want to search, we get the k position of the element using the same hash functions. If all of the bits at these positions are 1, we conclude that the element is probably in the dataset. However, if at least one position contains 0, we conclude that the element is definitely not in the dataset.

Bloom Filter Operations

1. Add

This operation refers to the addition of a new element to the dataset. This is one of the ways to update the Bloom Filter to add elements to the dataset.

Adding is done with these steps:

1. An element (for example, element X) that we want to add to the dataset is determined.
2. For Element X, k different hash functions are used in the Bloom Filter.
3. Each hash function determines k different positions of element X in the m-bit Bloom Filter.
4. The bits at these specified positions are marked as 1 (set).
5. The Bloom Filter is updated to represent the dataset containing element X.

These steps provide the ability of the Bloom Filter to detect the presence of a particular element by marking the element in its possible positions. However, it should be noted that the Bloom Filter has a feature that the probability of false positives increases as you add elements. Therefore, it is important to use it when the answers are imprecise and the probability of false positive results is acceptable.

2. Search

The search operation is used to query whether an element exists in the Bloom Filter. The Bloom Filter is designed to determine the probability of an element’s presence at high speed, but imprecise answers are acceptable. That is, rather than saying whether an element is definitely present in the filter, it means that it probably exists or is definitely not present.

The search is performed with these steps:

1. To check the existence of the element we want to search (for example, element Y), k different hash functions are used in the Bloom Filter.
2. Each hash function determines k different positions of element Y in the Bloom Filter.
3. The values of the bits in these specified positions are checked. If the bits at all positions are 1, it is concluded that element Y is probably inside the filter. However, if the bit in at least one position is 0, it is concluded that element Y is definitely not inside the filter.

The query process works effectively on large datasets thanks to its fast and low memory usage. However, the uncertainty of the answers and the possibility of false positive results should be considered.

False Positives

The concept of False Positive means that an element in the Bloom Filter is answered that it exists as a result of the query process, although it is not in the filter. That is, an element that is not actually in the dataset returns a positive result in the Bloom Filter query.

These misleading positive results are mainly due to the relationship between the size of the Bloom Filter (m), the number of hash functions (k), and the size of the dataset. The size (m) of the filter and the number of hash functions used (k) affect the probability of a Bloom Filter’s false positive. The false positive rate is related to the fill rate of the filter and the distribution of hash functions.

False positive results may or may not be acceptable depending on the type of application and sensitivity requirements. For example, if an element not found in a dataset is accidentally found to exist in the filter, this can have serious implications for the application. Therefore, the tolerance level of the possibility of false positives and its suitability to the application scenario should be taken into account when using the Bloom Filter.

Methods such as using a larger Bloom Filter, using more hash functions, or optimizing the size of the dataset can be applied to reduce the possibility of false positives. However, such fixes can often increase Bloom Filter’s memory and processor usage. Therefore, other data structures or filtering methods should be preferred to reduce the probability of false positives and where false positives are unacceptable.

Bloom Filter implementation in GoLang:

package main

import (
	"fmt"
	"hash/fnv"
)

type BloomFilter struct {
	bitArray []bool
	hashFunc []func(string) uint32
}

func NewBloomFilter(size int, numHashFunc int) *BloomFilter {
	bitArray := make([]bool, size)
	hashFunc := make([]func(string) uint32, numHashFunc)

	for i := 0; i < numHashFunc; i++ {
		hashFunc[i] = createHashFunc(i, size)
	}

	return &BloomFilter{
		bitArray: bitArray,
		hashFunc: hashFunc,
	}
}

func (bf *BloomFilter) Add(item string) {
	for _, hf := range bf.hashFunc {
		index := hf(item) % uint32(len(bf.bitArray))
		bf.bitArray[index] = true
	}
}

func (bf *BloomFilter) Contains(item string) bool {
	for _, hf := range bf.hashFunc {
		index := hf(item) % uint32(len(bf.bitArray))
		if !bf.bitArray[index] {
			return false
		}
	}
	return true
}

func createHashFunc(seed int, size int) func(string) uint32 {
	return func(data string) uint32 {
		hash := fnv.New32a()
		hash.Write([]byte(data))
		return uint32(seed) + hash.Sum32()%uint32(size)
	}
}

func main() {
	filter := NewBloomFilter(20, 3)

	// Adding elements to the filter
	filter.Add("apple")
	filter.Add("banana")
	filter.Add("orange")

	// Querying whether elements belong to the filter
	fmt.Println(filter.Contains("apple"))  // true
	fmt.Println(filter.Contains("banana")) // true
	fmt.Println(filter.Contains("orange")) // true
	fmt.Println(filter.Contains("grape"))  // false (false positive)
	fmt.Println(filter.Contains("cherry")) // false (false positive)
}

In this code sample, a simple Bloom Filter is implemented. When creating the Bloom Filter with the NewBloomFilter function, the filter size (size) and the number of hash functions to be used (numHashFunc) are specified. With the Add function, the elements are added to the filter and with the Contains function, it is questioned whether the elements are in the filter. The createHashFunc function is used to generate hash functions and a simple FNV (Fowler-Noll-Vo) hash algorithm is used.

When the program is run, the output will be as follows.

true
true
true
false
true

The running version of the program can be accessed from here.

Usage Areas

Bloom Filter is a preferred data structure in various usage areas due to its specific features. Below are some areas where the Bloom Filter is commonly used:

1. Database and Cache Management: It is used to make quick queries on large databases. In particular, to speed up possible queries in the database or not yet created, the Bloom Filter makes the database load less. Likewise, it is frequently used in cache management.
2. URL History in Web Browsers: In web browsers, the Bloom Filter can be used to keep in mind the URLs or web pages visited. This helps crawlers to query the pages visited more quickly.
3. Distributed Systems: In distributed systems, it is used to quickly query the existence of data. For example, the Bloom Filter can be used to check for the existence of keys in distributed file systems or distributed key-value storage systems.
4. Spam Filtering: In email or messaging applications, Bloom Filter can be used to quickly filter out spam emails or spam messages. Thus, spam filtering operations can be performed faster.
5. Graph and Network Algorithms: Bloom Filter can be preferred to speed up certain data structures used in graphs and network algorithms. For example, it can be used to check the presence of nodes in a graph data structure or to track connections in the network.
6. Memory Efficient Applications: Bloom Filter consumes less memory than other data structures. Therefore, it is preferred in applications where memory efficiency is important.

Resources

• https://en.wikipedia.org/wiki/Bloom_filter
• https://www.baeldung.com/cs/bloom-filter
• https://systemdesign.one/bloom-filters-explained/
• https://www.enjoyalgorithms.com/blog/bloom-filter
• https://brilliant.org/wiki/bloom-filter/#:~:text=A%20bloom%20filter%20is%20a,is%20added%20to%20the%20set.