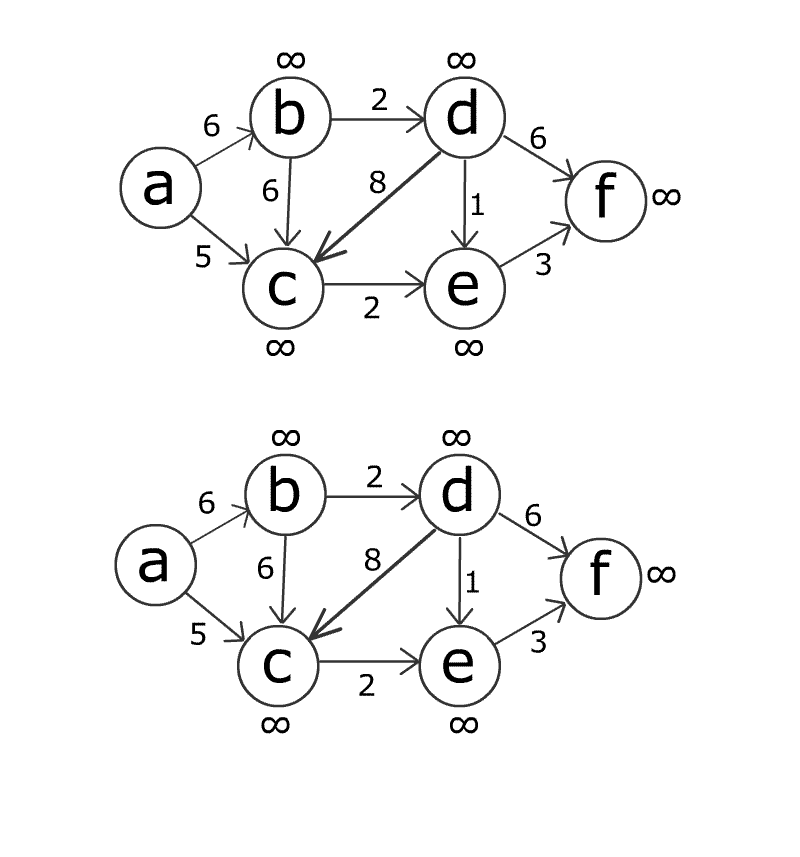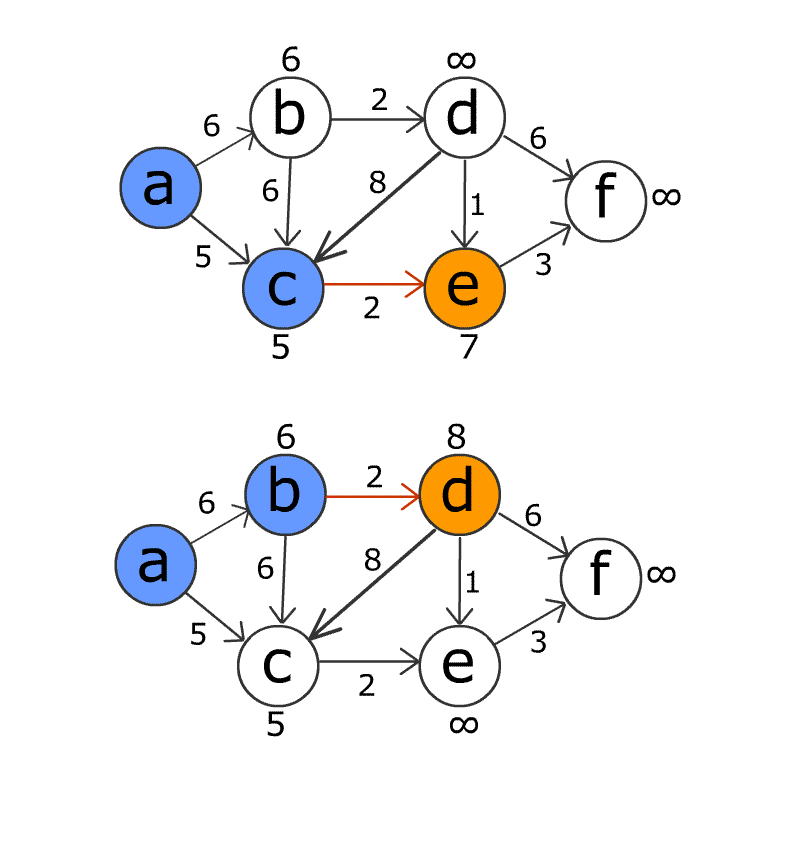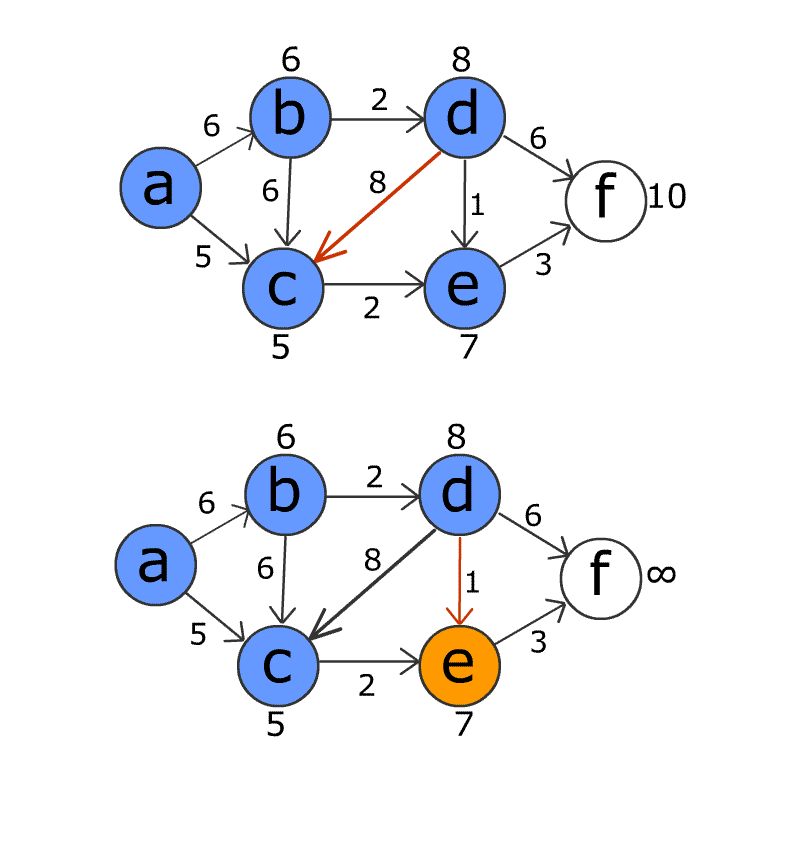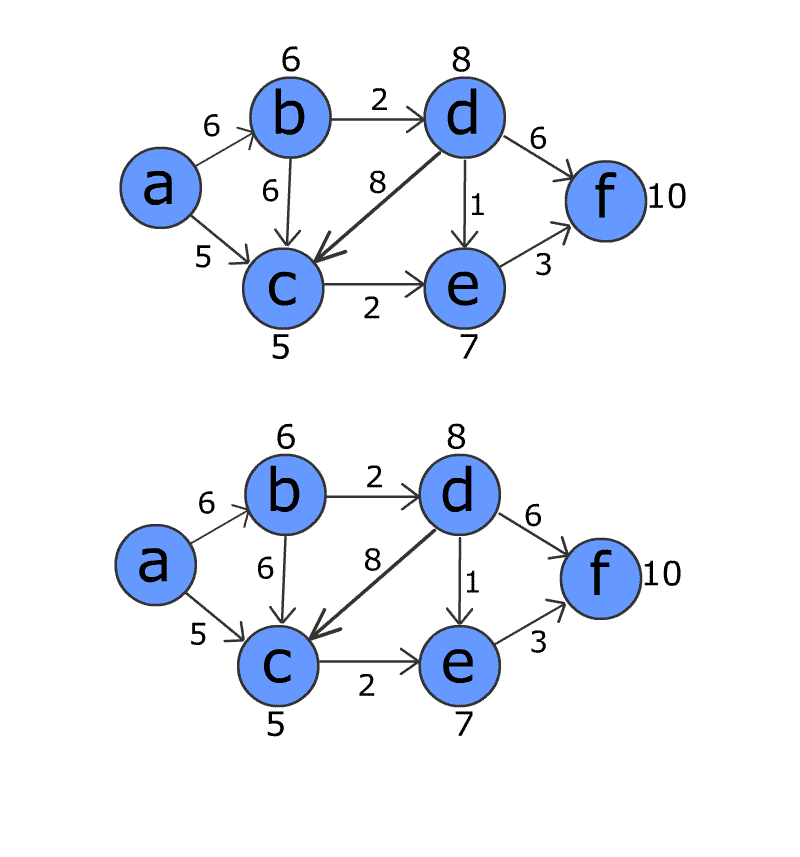
The Bellman-Ford algorithm is an algorithm used to solve the shortest path problem in a weighted graph. The shortest path problem is the problem of finding the shortest path from a starting point to a destination. The Bellman-Ford algorithm finds the shortest path by examining all possible path combinations. This algorithm can also handle situations such as graphs with negatively weighted edges, so it has a more general use unlike Dijkstra’s algorithm.

The working principle of the Bellman-Ford algorithm is as follows:

1. Set the distances to the starting point as infinity and the distance to itself as 0.
2. Review all edges and weights and update the distance of a path from the start point to the destination point for each edge.
3. Repeat this operation for the total number of nodes - 1 time. The reason it is done N times is the fact that the shortest path can pass through at most N-1 edges. If shorter paths can still be updated after n times, it indicates that the graph has a negatively weighted loop.

Dijkstra’s algorithm is a fast-running algorithm to find the shortest path on positive weighted graphs or edges. At each step, the node with the smallest distance is selected and operates. On the other hand, the Bellman-Ford algorithm can be used on negative or positive weighted graphs and edges and has a more general use. It finds the shortest path by going through all the edges and weights step by step, but may require more time as it examines all the edges at each step. Therefore, while Dijkstra generally works faster, the Bellman-Ford algorithm can handle a wider range of problems and can also handle negatively weighted graphs or edges.

Complexity

• Worst-case performance O(|V||E|)
• Best-case performance O(|E|)
• Worst-case space complexity O(|V|)

Bellman–Ford Algorithm implementation in GoLang:

package main

import (
	"fmt"
	"math"
)

type Edge struct {
	Source int
	Target int
	Weight int
}

func BellmanFord(edges []Edge, vertexCount int, start int) ([]int, []int) {
	distances := make([]int, vertexCount)
	predecessors := make([]int, vertexCount)

	for i := range distances {
		distances[i] = math.MaxInt32
	}
	distances[start] = 0

	for i := 1; i < vertexCount; i++ {
		for _, edge := range edges {
			if distances[edge.Source]+edge.Weight < distances[edge.Target] {
				distances[edge.Target] = distances[edge.Source] + edge.Weight
				predecessors[edge.Target] = edge.Source
			}
		}
	}

	for _, edge := range edges {
		if distances[edge.Source]+edge.Weight < distances[edge.Target] {
			fmt.Println("Negative cycle detected. Bellman-Ford algorithm cannot be applied.")
			return nil, nil
		}
	}

	return distances, predecessors
}

func main() {
	vertexCount := 5
	edges := []Edge{
		{0, 1, 2},
		{0, 2, 4},
		{1, 2, 1},
		{1, 3, 7},
		{2, 4, 3},
		{3, 4, 1},
	}

	startNode := 0
	distances, predecessors := BellmanFord(edges, vertexCount, startNode)

	if distances != nil {
		fmt.Println("Shortest distances from node", startNode)
		for i, distance := range distances {
			fmt.Printf("Node %d: Distance %d, Path: ", i, distance)
			path := []int{}
			for at := i; at != startNode; at = predecessors[at] {
				path = append([]int{at}, path...)
			}
			path = append([]int{startNode}, path...)
			fmt.Println(path)
		}
	}
}

When the program is run, the output will be as follows.

Shortest distances from node 0
Node 0: Distance 0, Path: [0]
Node 1: Distance 2, Path: [0 1]
Node 2: Distance 3, Path: [0 1 2]
Node 3: Distance 9, Path: [0 1 2 4 3]
Node 4: Distance 6, Path: [0 1 2 4]

The running version of the program can be accessed at here.

Resources

• https://en.wikipedia.org/wiki/Bellman%E2%80%93Ford_algorithm
• https://www.baeldung.com/cs/bellman-ford